Algorithm design

28th of January, 2019 in notes

Reading notes from “The Algorithm Design manual” book written by Steven S. Skiena.

1. Definitions
   1. Proper mathematical proof:
   2. Algorithmic notations:
   3. Problem specification:
   4. Correctness: induction & recursion
   5. Modeling the problem
      1. Combinatorial objects
         1. Permutations
         2. Subsets
         3. Trees
         4. Graphs
         5. Points
         6. Polygons / polyhedron
         7. Strings
      2. Recursive objects

Definitions

Proper mathematical proof:

1. Clear & precise statement of what you are trying to prove
2. Set of assumptions which are taken to be true
3. Chain of reasonning takes you from the assumptions to the statement you are trying to prove
4. QED

Algorithmic notations:

• English
• Pseudo code
• Real programming language

Heart of an algorithm is an idea. This idea must be clearly revealed when the algorithm is expressed.

Problem specification:

• Set of allowed input instances
• Required properties of the algorithm’s output

Counter-examples to demonstrate incorrectness

Develop counter-examples hunting skill:

• Think small
• Think exhaustively
• Hunt for the weakness
• Go for a tie
• Seek extremes

Correctness: induction & recursion

• Induction:
  • Prove a formula, for example \(\sum_{i=1}^n = \frac{ n(n+1) }{2}\) work for basis cases (like 1 or 2)
  • Assume it was true up to \(n-1\)
  • Prove is was true to general \(n\) using the assumption
• Recursion is induction
  • General & boundary conditions, with the general condition breaking the problem into smaller and smaller pieces

Have to be suspicious about induction.

• Boundary errors
• Wrong extension claims (for example, adding an item that completely changes the solution of a problem)

e.g. Prove that \(\sum_{i=1}^n i \times i! = (n+1)!-1\) by induction

1. \(n=1\) \begin{align*} \sum_{i=1}^n i \times i! &= 1 \times 1 \
   &= 1 \end{align*}  
   \begin{align*} (n+1)!-1 &= 2! - 1 \
   &= 1 \end{align*}

2. Assume the statement is true up to \(n\). Prove that it is also true for \(n+1\) \begin{align*} \sum_{i=1}^{n+1} i \times i! &= (n+1) \times (n+1)! + \sum_{i=1}^n i \times i! \
   &= (n+1) \times (n+1)! + (n+1)!-1 \
   &= (n+1)! \times ( (n+1) + 1 ) -1 \
   &= (n+1)! \times ( n+2 ) -1 \
   &= (n+2)! -1 \
   &\blacksquare \end{align*}

Modeling the problem

Try to describe the problem abstractly, in terms of procedures on fundamental structures (e.g. permutatons, graphs, sets …)

Combinatorial objects

Permutations

Arrangements, ordering of items. \(\left\{1,4,3,2\right\}\) and \(\left\{4,3,2,1\right\}\) are two distinct permutations of the same set of four integers. Likely to be used when talking about “arrangement”, “tour”, “ordering” or “sequence”.

Subsets

Selection from a set of items. \(\left\{1,4,3\right\}\) and \(\left\{2\right\}\) are two subsets of the first four integers. Order does not matter in subsets, so the subsets \(\left\{1,4,3\right\}\) and \(\left\{4,3,1\right\}\) would be considered identical. Likely to be used when talking about “cluster”, “collection”, “committee”, “group”, “packaging” or “selection”.

Trees

Represent hierarchical relationships between items.

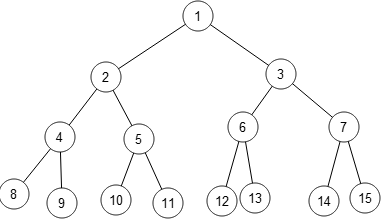
Likely to be used when talking about “hierarchy”, “dominance”, “relationship”, “ancestor/descendant relationship” or “taxonomy”.

Graphs

Represent relationships between arbitrary pair of objects.

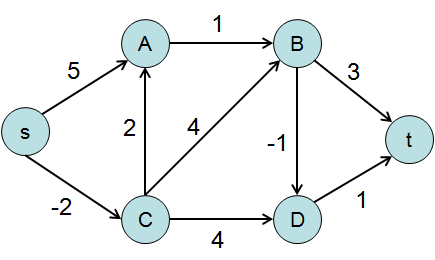
Points are called vertices and links edges.

Likely to be used when talking about “network”, “circuit”, “web”, or “relationship”.

Points

Represent location in some geometric space. Likely to be used when talking about “sites”, “positions”, “data records”, or “locations”.

Polygons / polyhedron

Represent regions in some geometric space. Likely to be used when talking about “shapes”, “regions”, “configurations”, or “boundaries”.

Strings

Represent sequences of characters or patterns. Likely to be used when talking about “text”, “characters”, “patterns”, or “labels”.

Modeling your application in terms of well-defined structures and algorithms is the most important single step toward a solution. Be aware that the act of modeling reduces your application to one of a small number of existing problems and structures.

Recursive objects

Big things made from smaller things of exactly the same type as the big thing.

Combinatorial objects are also recursive.

Recursive descriptions of objects require both decomposition rules and basis cases.